
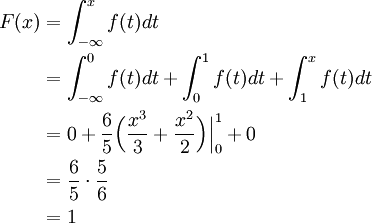


The PDF is only really useful for quickly ascertaining where the peak of a distribution is and getting a rough sense of the width and shape (which give a visual understanding of Variance and Skewness). I know you're thinking: "I do so much love taking all these integrals each time I have different question!" But let's make the radical assumption that you'd prefer to just look at a plot and get these answers! Despite its ubiquity in probability and statistics, the PDF is actually a pretty mediocre way to look at data. This means that the probability that our conversion rate is much higher than we observed is actually a bit more likely that the probability that it is much less than observed! Introducing the Cumulative Distribution Function! What does this PDF represent? From our data we can infer that our average conversion rate is simply \(\fracBeta(300,39700) \approx 0.012$$ We can visualize the Probability Density Function (PDF) for this Beta Distribution as follows: That would be \(Beta(300,39700)\) (remember \(\beta\) is the number of people who did not subscribe, not the total). In this case, let's say for first 40,000 visitors I get 300 subscribers. There are two parameters for the Beta distribution, \(\alpha\) in this case representing the total subscribed (\(k\)), and \(\beta\) representing the total not subscribed (\(n-k\)). If you read the earlier post on Discrete and Continous Probability distributions you'll know that the way we can determine \(p\), the probability of subscribing given that we know \(k\), the number of people subscribed and \(n\) the total number of people who visited is to use the Beta distribution. In marketing terms getting a user to perform a desired event is referred to as the conversion event or simply a conversion and the probability that a user will convert is the conversion rate. Trying to figure out this missing parameter is referred to as Parameter Estimation.įor example suppose I want to know what the probability is that a visitor to this blog will subscribe to the email list ( do it for science!). In reality the inverse is much more common: we have data about the outcomes but don't really know what the true probability of the event is. When we start learning probability we often are told the probability of an event and from there try to estimate the likelihood of various outcomes. This post is part of our Guide to Bayesian Statistics and an updated version is included in my new book Bayesian Statistics the Fun Way !


 0 kommentar(er)
0 kommentar(er)
